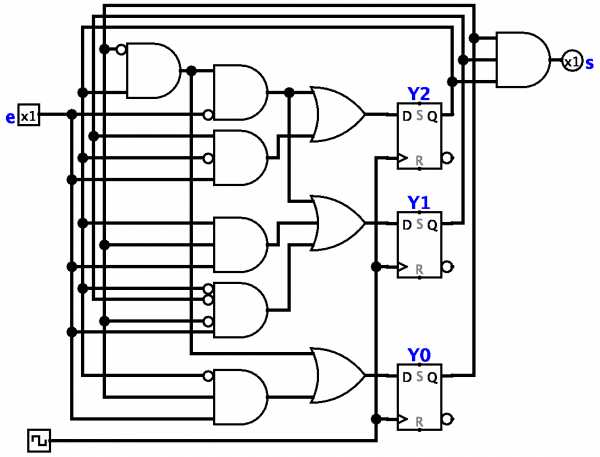
Теорија аутомата, коначни аутомати
Структура, дизајн, принцип рада различитих машина у великој мери су одређени његовом функционалном наменом. Разликовати технолошке, транспортне, рачунарске, војне и друге машине. Целокупни аутоматски комплекси дизајнирани за обављање сложених технолошких процеса широко се користе у различитим индустријама. Пројектовани су и изграђени аутомати који обављају различите логичке функције (логичке машине).
Теорија аутомата — секција кибернетике, који је настао под утицајем захтева технологије дигиталних рачунара и управљачких машина. Дискретни аутомати који се проучавају у теорији аутомата су апстрактни модели реалних система (техничких и биолошких) који обрађују дискретне (дигиталне) информације у дискретним временским корацима.
Теорија аутомата се заснива на прецизним математичким концептима који формализују интуитивне идеје о функционисању (понашању) аутомата и о његовој структури (унутрашњој структури).
У овом случају, трансформација информација се увек схвата као операција која трансформише улазне секвенце састављене од слова из улазног алфабета у излазне секвенце састављене од слова из излазне абецеде.
Апарат математичке логике, алгебре, теорије вероватноће, комбинаторике и теорије графова има широку примену.
Проблем са теоријом аутомата у неким њеним деловима (структурна теорија аутомата) је растао из теорије релејно-контактних кола, који је почео да се обликује крајем 1930-их. инклузивно методе логичке алгебре.

У структурној теорији аутомата проучавају се различите врсте шема које су дизајниране да опишу како се сложени аутомат ствара од једноставнијих компоненти (елемената) правилно повезаних у систем.
Други правац, назван апстрактна теорија аутомата, проучава понашање аутомата (то јест, природу трансформације информација коју они врше), апстрахујући од специфичности њихове унутрашње структуре, а настао је 1950-их.
У оквиру апстрактне теорије аутомата, садржај појмова „аутомат“ и „машина“ суштински се исцрпљује стандардним описом трансформације информација коју врши аутомат. Таква трансформација може бити детерминистичка, али може бити и вероватноћа по природи.
Највише проучаване су детерминистичке машине (аутомати), у које спадају коначни аутомати — главни предмет проучавања у теорији аутомата.
Коначну машину карактерише ограничена количина меморије (број унутрашњих стања) и дефинисана је помоћу прелазне функције.Уз неку разумну идеализацију, све савремене математичке машине, па чак и мозак, са становишта њиховог функционисања, могу се сматрати коначним аутоматима.
Термини „секвенцијална машина“, „Милијев аутомат“, „Муров аутомат“ се у литератури (и не уједначено код свих аутора) користе као синоними појма „коначни аутомат“ или да би се истакле одређене особине у прелазним функцијама коначног аутомата. аутомат.
Аутомати са неограниченом меморијом су Турингова машина способна да изврши (потенцијално) било коју ефикасну трансформацију информација. Концепт "Тјурингове машине" настао је раније од концепта "коначне машине" и углавном се проучава у теорији алгоритама.
Апстрактна теорија аутомата је уско повезана са добро познатим алгебарским теоријама, на пример теоријом полугрупа. Са примењене тачке гледишта, од интереса су резултати који карактеришу трансформацију информација у аутомату у смислу величине меморије.
То је случај, на пример, у проблемима са експериментима на аутоматима (радови Е.Ф. Моореа, итд.), где се једна или она информација о прелазним функцијама аутомата или о капацитету његове меморије добијају из резултата експерименти.
Други задатак је израчунавање периода излазних секвенци, на основу доступних информација о величини меморије аутомата и периодима улазних секвенци.
Од великог значаја је развој метода за минимизирање меморије коначних машина и проучавање њиховог понашања у насумичним окружењима.
У теорији апстрактних аутомата, проблем синтезе је следећи.У терминима неког јасно формализованог језика, записани су услови за понашање пројектованог аутомата (за догађај представљен у аутомату). У овом случају, потребно је развити методе које према сваком написаном услову:
1) сазнати да ли постоји таква државна машина да информације које се њиме трансформишу испуњавају овај услов;
2) ако јесте, онда се конструишу прелазне функције такве машине коначног стања или се процењује њена величина меморије.
Решење задатка синтезе у таквој формулацији претпоставља претходно стварање погодног језика за снимање услова рада аутомата са погодним алгоритмима за прелазак са снимања на транзитивне функције.
У структурној теорији аутомата, проблем синтезе се састоји у конструисању ланца елемената датог типа који реализује коначни аутомат дат његовим прелазним функцијама. У овом случају обично наводе неки критеријум оптималности (на пример, минимални број елемената) и настоје да добију оптималну шему.
Како се касније испоставило, то значи да су неки од метода и концепата који су раније развијени у вези са релејно-контактним круговима применљиви на кола другог типа.
У вези са развојем електронских технологија, најраспрострањеније су шеме функционалних елемената (логичке мреже). Посебан случај логичких мрежа су апстрактне неуронске мреже, чији се елементи називају неурони.
Развијене су многе методе синтезе у зависности од врсте кола и трансформације информација за коју су намењена (Синтеза релејних уређаја).
Погледај -Минимизација комбинационих кола, Карноове карте, синтеза кола
Коначна машина — математички модел управљачког система са фиксном (неспособном да се повећава током рада) величином меморије.
Концепт машине коначног стања је математичка апстракција која карактерише опште карактеристике скупа управљачких система (на пример, релејни уређај са више петљи). Сви такви системи имају заједничке карактеристике које је природно прихватити као дефиницију коначног аутомата.
Сваки завршени аутомат има улаз изложен спољашњим утицајима и унутрашњим елементима. И за улазне и за унутрашње елементе, постоји фиксни број дискретних стања која могу да заузму.
Промена стања улазних и унутрашњих елемената дешава се у дискретним тренуцима времена, интервали између којих се називају тикови. Унутрашње стање (стање унутрашњих делова) на крају траке је у потпуности одређено унутрашњим стањем и стањем улаза на почетку траке.
Све остале дефиниције коначног аутомата могу се свести на ову карактеристику, посебно дефиниције које претпостављају да коначни аутомат има излаз који зависи од унутрашњег стања аутомата у датом тренутку.
У смислу такве карактеристике, природа његових улаза и унутрашњих стања је ирелевантна за опис комплетног аутомата. Уместо улаза и стања, можете само да погледате њихове бројеве у случајном нумерисању.
Машина стања ће бити постављена ако је наведена зависност њеног интерног броја стања од претходног интерног броја стања и претходног улазног броја стања. Такав задатак може бити у форми завршне табеле.
Други уобичајен начин дефинисања комплетног аутомата је конструкција тзв дијаграми прелаза. Улазна стања се често називају једноставно улазима, а унутрашња стања су једноставно стања.
Машина коначног стања може бити модел и техничких уређаја и неких биолошких система. Аутомати првог типа су, на пример, релејни уређаји и разни електронски рачунари, укљ. програмабилни логички контролери.
У случају релејног уређаја, улогу улазних стања имају комбинације стања осетљивих елемената релејног уређаја (свака комбинација таквих стања је „сложено стање“, које карактерише индикација свих осетљивих елемената ова дискретна стања која имају у датом тренутку). Слично, комбинације стања међуелемента релејног уређаја делују као унутрашња стања.
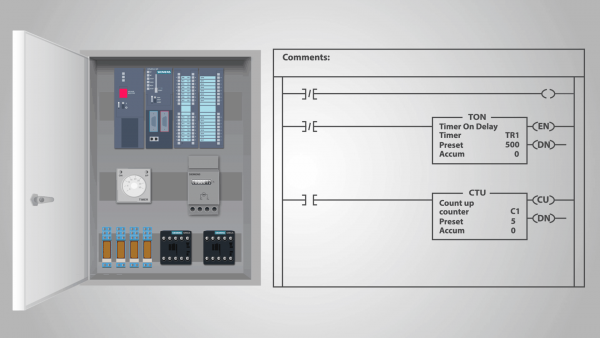
Програмабилни логички контролер (ПЛЦ) је пример релејног акционог уређаја који се може назвати самосталном државном машином.
У ствари, када је програм унет у ПЛЦ и контролер је почео да рачуна, он није изложен спољним утицајима и свако следеће стање је у потпуности одређено његовим претходним стањем. Можемо претпоставити да улаз има исто стање у сваком циклусу такта.
Насупрот томе, свака машина коначног стања која има једино могуће улазно стање се природно назива аутономном, пошто у овом случају спољашње окружење не носи информације које контролишу његово понашање.
Такође видети:
Примена микропроцесорских система у електротехници на примеру употребе ПЛЦ-а