Шта је магнетомоторна сила, Хопкинсонов закон

У другој половини 19. века енглески физичар Џон Хопкинсон и његов брат Едвард Хопкинсон, развијајући општу теорију магнетних кола, извели су математичку формулу под називом „Хопкинсонова формула“ или Хопкинсонов закон, који је аналог Омовог закона (у употреби за прорачун електричних кола).

Дакле, ако Омов класични закон математички описује однос између струје и електромоторне силе (ЕМС), Хопкинсонов закон на сличан начин изражава однос између магнетног флукса и тзв. магнетомоторна сила (МДФ).

Као резултат тога, испоставило се да магнетомоторна сила је физичка величина која карактерише способност електричних струја да стварају магнетне флуксове. И Хопкинсонов закон у том погледу може се успешно користити у прорачунима магнетних кола, пошто је МДФ у магнетним колима аналоган ЕМФ у електричним колима. Датумом открића Хопкинсоновог закона сматра се 1886. година.

Величина магнетомоторне силе (МДФ) се у почетку мери у амперима или, ако говоримо о завојници са струјом или електромагнетом, онда за погодност прорачуна користите њен израз у ампер-завојима:

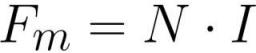
где је: Фм магнетомоторна сила у калему [ампер * завој], Н је број завоја у калему [завој], И је количина струје у сваком од завоја калема [ампер].

Ако овде унесете вредност магнетног флукса, онда ће Хопкинсонов закон за магнетно коло имати следећи облик:

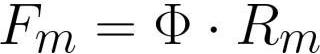
где је: Фм магнетомоторна сила у калему [ампер * окрет], Ф је магнетни флукс [вебер] или [хенри * ампер], Рм је магнетни отпор проводника магнетног флукса [ампер * окрет / вебер] или [ турн / Хенри] .

Текстуална формулација Хопкинсоновог закона првобитно је била следећа: „у неразгрананом магнетном колу, магнетни флукс је директно пропорционалан магнетомоторној сили и обрнуто пропорционалан укупном магнетном отпору“. То јест, овај закон одређује однос између магнетомоторне силе, релуктанције и магнетног флукса у колу:

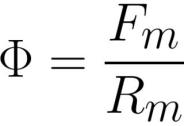
овде: Ф је магнетни флукс [вебер] или [хенри * ампер], Фм је магнетомоторна сила у калему [ампер * обрт], Рм је магнетни отпор проводника магнетног флукса [ампер * револуција / вебер] или [ турн / Хенри] .

Овде је важно напоменути да у ствари магнетомоторна сила (МДФ) има фундаменталну разлику од електромоторне силе (ЕМФ), која се састоји у чињеници да се ниједна честица не креће директно у магнетном флуксу, док струја настаје под дејством ЕМФ преузима кретање наелектрисаних честица, на пример електрона у металним жицама. Међутим, идеја МДС-а помаже у решавању проблема израчунавања магнетних кола.

Размотримо, на пример, неразгранано магнетно коло које укључује јарам површине попречног пресека С, исти по целој дужини, а материјал јарма има магнетну пермеабилност му.

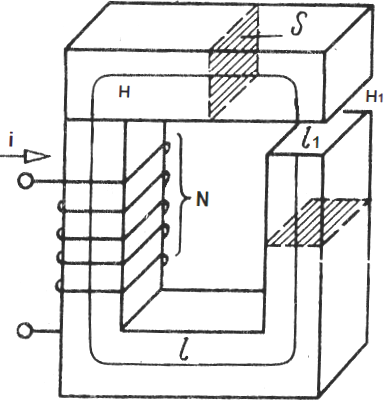
Зазор у јарму - различит материјал, магнетна пермеабилност који му1. Завојница постављена на јарам садржи Н завоја, струја и тече кроз сваки од навојака завојнице. Примењујемо теорему о циркулацији магнетног поља на средишњу линију јарма:

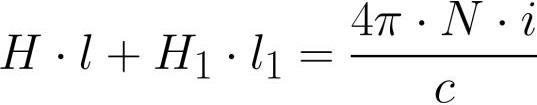
где је: Х јачина магнетног поља унутар јарма, Х1 је јачина магнетног поља унутар отвора, л је дужина средишње линије индукције јарма (без зазора), л1 је дужина процепа.

Пошто магнетни флукс унутар јарма и унутар процепа има исту вредност (због континуитета водова магнетне индукције), после записивања Ф = БС и В = му * Х, записаћемо јачину магнетног поља детаљније , а након замени ово у горњу формулу:

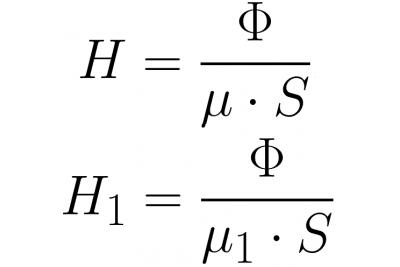
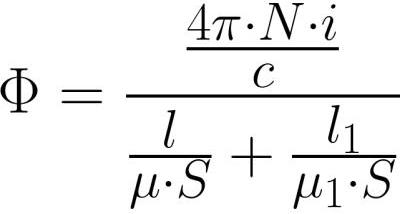
Лако је видети да је, као и ЕМФ у Омовом закону за електрична кола, МДС

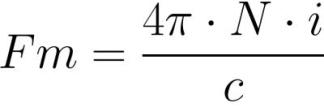
овде игра улогу електромоторне силе и магнетног отпора

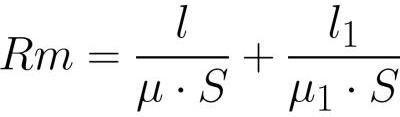
улога отпора (по аналогији са класичним Омовим законом).