Електрони се понашају као таласи

Физичари одавно знају да је светлост електромагнетни талас. До данас нико не сумња у ову позицију, пошто светлост јасно показује све знаке понашања таласа: светлосни таласи могу да се преклапају, стварајући интерферентни образац, такође су у стању да се одвоје, савијајући се око препрека дуж времена дифракције.

Када видимо птицу која хода као патка, плива као патка и квоца као патка, ту птицу називамо патка. Дакле, светлост је електромагнетни таласна основу објективно уочених знакова понашања таквог таласа у светлости.

Међутим, крајем 19. и 20. века, физичари су почели да говоре о „дуализму честица-талас” светлости. Испоставило се да сазнање да је светлост електромагнетни талас није све што наука зна о светлости. Научници су открили веома занимљиву особину у светлости.

Испоставило се да се светлост некако манифестује КАО понашање струје честица.Утврђено је да се енергија коју носи светлост, након што је у одређеном временском периоду изброји посебним детектором, ионако састоји од појединачних (целих) делова.

Стога је постало тачно да је енергија светлости дискретна, јер је састављена, такорећи, од појединачних честица – „кванта“, односно од најмањих целих порција енергије. Таква честица светлости, која носи јединицу (или квант) енергије, почела је да се зове фотон.

Енергија једног фотона се налази по следећој формули:

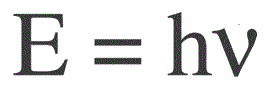
Е — енергија фотона, х — Планкова константа, в — фреквенција.

Немачки физичар Макс Планк је први експериментално утврдио чињеницу дискретности светлосног таласа и израчунао вредност константе х која се појављује у формули за проналажење енергије појединачних фотона. Испоставило се да је ова вредност: 6,626 * 10-34 Ј * с. Планк је објавио резултате свог рада крајем 1900-их.

Размотрите, на пример, љубичасти зрак. Фреквенција такве светлости (ф или в) је 7,5 * 1014 Хз Планкова константа (х) је 6,626 * 10-34 Ј * с. То значи да је енергија фотона, (Е), карактеристична за љубичасту боју, 5 * 10-19 Ј. Ово је тако мали део енергије да је веома тешко ухватити.

Замислите планински поток — он тече као једна целина и немогуће је видети голим оком да је поток заправо сачињен од појединачних молекула воде. Данас, међутим, знамо да је макроскопски објекат — ток — заправо дискретан, односно да се састоји од појединачних молекула.

То значи да ако можемо да поставимо бројач молекула поред потока да броји молекуле воде који пролазе док струја тече, детектор ће увек бројати само цео број молекула воде, а не делимичне.

Слично томе, график укупне енергије фотона Е, израчунат у тренутку т — увек ће се показати да није линеаран (жута фигура), већ поступно (зелена фигура):

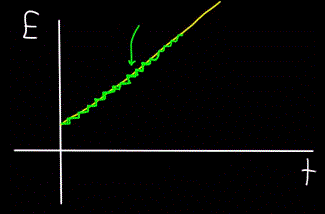
Дакле, фотони се крећу, они носе енергију, стога имају импулс. Али фотон нема масу. Како онда можете пронаћи замах?

У ствари, за објекте који се крећу брзином блиском брзини светлости, класична формула п = мв је једноставно неприменљива. Да бисмо разумели како пронаћи замах у овом необичном случају, окренимо се специјалној релативности:

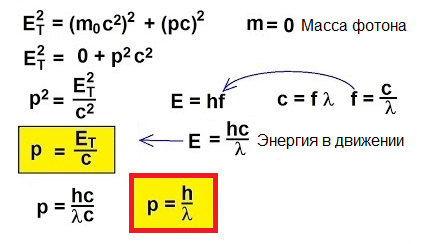
1905. Алберт Ајнштајн је објаснио са ове тачке гледишта фотоелектрични ефекат… Знамо да метална плоча има електроне у себи, који унутар ње привлаче позитивно наелектрисана језгра атома и стога се задржавају у металу. Али ако такву плочу засијате светлошћу ОДРЕЂЕНЕ фреквенције, онда можете да избаците електроне из плоче.

Као да се светлост понаша као ток честица са импулсом.И иако фотон нема масу, он ипак некако интерагује са електроном у металу, и под одређеним условима фотон може да избаци електрон.

Дакле, ако фотон који упадне на плочу има довољно енергије, онда ће електрон бити избачен из метала и померити се из плоче брзином в. Такав избачени електрон назива се фотоелектрон.

Пошто избијени електрон има познату масу м, имаће одређену кинетичку енергију мв.

Енергија фотона, када делује на метал, претвара се у енергију изласка електрона из метала (радна функција) и у кинетичку енергију електрона, поседујући коју избијени електрон почиње да се креће. из метала, остављајући га.

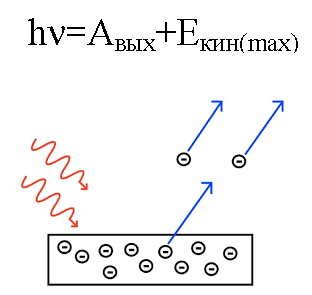
Претпоставимо да фотон познате таласне дужине удари у површину метала за коју је позната радна функција (електрона из метала). У овом случају се лако може наћи кинетичка енергија електрона емитованог из датог метала, као и његова брзина.

Ако енергија фотона није довољна да електрон изврши радну функцију, онда електрон једноставно не може напустити површину датог метала и фотоелектрон се не формира.

1924. француски физичар Лоуис де Броглие изнео продорну идеју према којој не само фотони светлости већ и сами електрони могу да се понашају као таласи. Научник је чак извео формулу за хипотетичку таласну дужину електрона. Ови таласи су касније названи "де Брољеви таласи".

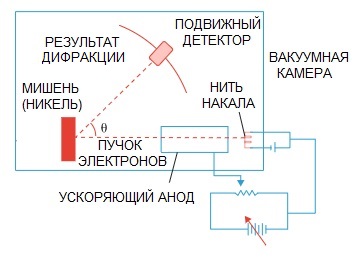
Де Брољева хипотеза је касније потврђена. Физички експеримент о дифракцији електрона, који су 1927. године извели амерички научници Клинтон Дејвисон и Лестер Гермер, коначно је указао на таласну природу електрона.

Када је сноп електрона усмерен кроз посебну атомску структуру, чини се да је детектор требало да сними слику као честице које лете једна за другом, што би се логично очекивало да су електрони честице.

Али у пракси имамо слику карактеристичну за дифракцију таласа. Штавише, дужине ових таласа су у потпуности у складу са концептом који је предложио де Брољ.

На крају, де Брољева идеја је омогућила да се објасни принцип Боровог атомског модела, а касније је омогућила Ервину Шредингеру да генерализује ове идеје и постави темеље модерне квантне физике.