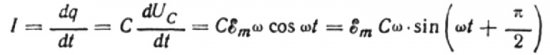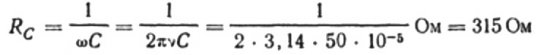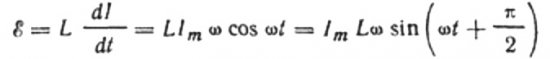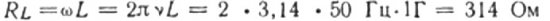Капацитивни и индуктивни отпор у колу наизменичне струје

Ако укључимо кондензатор у једносмерно коло, открићемо да он има бесконачан отпор јер једносмерна струја једноставно не може да прође кроз диелектрик између плоча, пошто диелектрик по дефиницији не спроводи једносмерну електричну струју.

Кондензатор прекида једносмерно коло. Али ако је исти кондензатор сада укључен у коло наизменичне струје, онда се испоставља да се његов кондензатор не поквари у потпуности, он се једноставно мења и пуни, односно електрични набој се креће, а струја у спољашњем колу је одржавана.

На основу Максвелове теорије у овом случају можемо рећи да је наизменична струја проводљивости унутар кондензатора и даље затворена, само у овом случају — струјом пристрасности. То значи да кондензатор у колу наизменичне струје делује као врста отпора коначних вредности. Овај отпор се зове капацитивни.

Пракса је одавно показала да количина наизменичне струје која тече кроз проводник зависи од облика тог проводника и од магнетних својстава средине око њега.Код праве жице струја ће бити највећа, а ако се иста жица намота у калем са великим бројем завоја, струја ће бити мања.

А ако се феромагнетно језгро уведе у исти калем, струја ће се још више смањити. Дакле, жица обезбеђује наизменичну струју не само са омским (активним) отпором, већ и са додатним отпором, у зависности од индуктивности жице.Овај отпор се назива индуктивни.

Његово физичко значење је да променљива струја у проводнику одређене индуктивности иницира ЕМФ самоиндукције у том проводнику, која тежи да спречи промене струје, односно да смањи струју. Ово је еквивалентно повећању отпора жице.

Капацитет у колу наизменичне струје

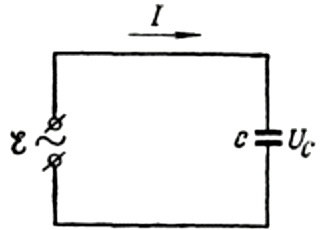
Прво, хајде да причамо о капацитивном отпору детаљније. Претпоставимо да је кондензатор капацитета Ц повезан са синусоидним извором наизменичне струје, тада ће ЕМФ овог извора бити описан следећом формулом:

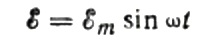
Пад напона на прикључним жицама ћемо занемарити, јер је обично веома мали и може се разматрати одвојено ако је потребно. Претпоставимо сада да је напон на плочама кондензатора једнак напону извора наизменичне струје. Онда:

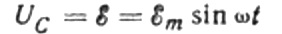
У сваком тренутку, наелектрисање кондензатора зависи од његовог капацитета и напона између његових плоча. Затим, с обзиром на познати извор који је горе поменут, добијамо израз за проналажење наелектрисања на плочама кондензатора према напону извора:

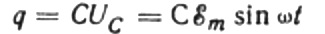
Нека се за бесконачно мало време дт наелектрисање на кондензатору промени за дк, тада ће струја И тећи кроз жице од извора до кондензатора једнака:

Вредност тренутне амплитуде биће једнака:

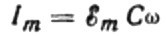
Тада ће коначни израз за струју бити:

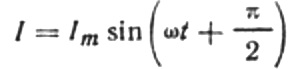
Хајде да препишемо формулу тренутне амплитуде на следећи начин:

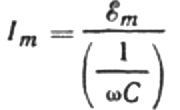
Овај однос је Омов закон, где реципрочна вредност производа угаоне фреквенције и капацитивности игра улогу отпора, а заправо је израз за проналажење капацитивности кондензатора у колу синусоидалне наизменичне струје:

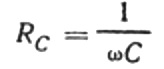
То значи да је капацитивни отпор обрнуто пропорционалан угаоној фреквенцији струје и капацитивности кондензатора. Лако је разумети физичко значење ове зависности.

Што је већи капацитет кондензатора у колу наизменичне струје и што се чешће мења смер струје у том колу, на крају више укупног наелектрисања пролази у јединици времена кроз попречни пресек жица које повезују кондензатор са извором наизменичне струје. То значи да је струја пропорционална производу капацитивности и угаоне фреквенције.

На пример, израчунајмо капацитивност кондензатора са електричним капацитетом од 10 микрофарада за синусоидно коло наизменичне струје са фреквенцијом од 50 Хз:

Ако је фреквенција 5000 Хз, онда би исти кондензатор имао отпор од око 3 ома.

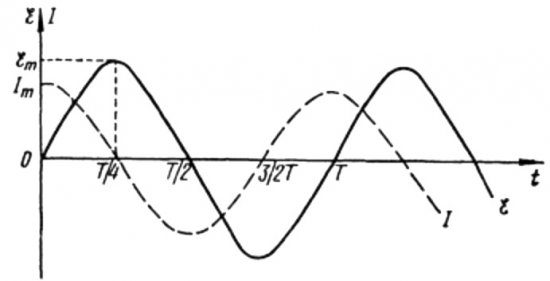
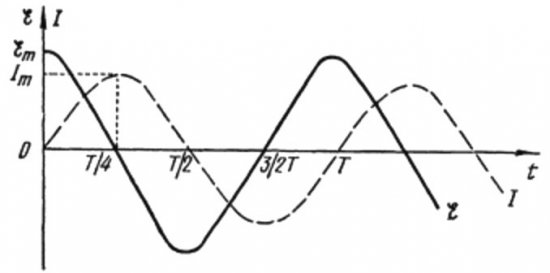
Из горњих формула је јасно да се струја и напон у наизменичном колу са кондензатором увек мењају у различитим фазама. Тренутна фаза води фазу напона за пи / 2 (90 степени). То значи да максимална струја у времену увек постоји четвртину периода раније од максималног напона. Дакле, преко капацитивног отпора, струја води напон за четвртину временског периода, или за 90 степени у фази.

Хајде да објаснимо физичко значење овог феномена.У првом тренутку, кондензатор је потпуно испражњен, тако да најмањи напон примењен на њега већ помера наелектрисања на плочама кондензатора, стварајући струју.

Како се кондензатор пуни, напон на његовим плочама се повећава, што спречава даљи ток пуњења, тако да се струја у колу смањује упркос даљем повећању напона примењеног на плоче.

То значи да ако је у почетном тренутку струја била максимална, онда када напон достигне свој максимум након четвртине периода, струја ће потпуно престати.

На почетку периода струја је максимална, а напон минималан и почиње да расте, али након четвртине периода напон достиже максимум, али је струја до тог тренутка већ пала на нулу. Тако се испоставља да напон предњачи напон за четвртину периода.

АЦ индуктивни отпор

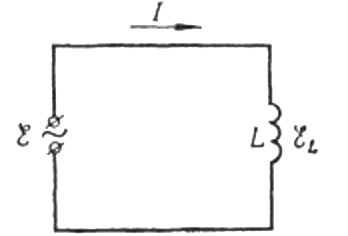
Сада се вратимо на индуктивни отпор. Претпоставимо да кроз калем индуктивности тече наизменична синусна струја. Може се изразити као:

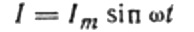
Струја настаје услед наизменичног напона који се примењује на калем. То значи да ће се на завојници појавити ЕМФ самоиндукције, који се изражава на следећи начин:

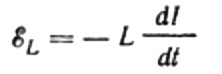
Опет, занемарујемо пад напона на жицама које повезују ЕМФ извор са калемом. Њихов омски отпор је веома низак.

Нека наизменични напон примењен на калем у било ком тренутку буде потпуно избалансиран насталим ЕМФ-ом самоиндукције који му је једнак по величини, али супротног смера:

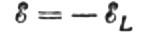
Онда имамо право да напишемо:

Пошто је амплитуда напона примењеног на калем:

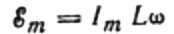
добијамо:

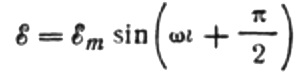
Изразимо максималну струју на следећи начин:

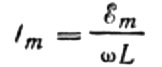
Овај израз је у суштини Омов закон. Количина једнака производу индуктивности и угаоне фреквенције овде игра улогу отпора и није ништа друго до индуктивни отпор индуктора:

Дакле, индуктивни отпор је пропорционалан индуктивности завојнице и угаоној фреквенцији наизменичне струје кроз тај калем.

Ово је због чињенице да је индуктивни отпор последица утицаја ЕМФ самоиндукције на напон извора, - ЕМФ самоиндукције тежи да смањи струју и стога доноси отпор у колу. Величина емф самоиндукције, као што је познато, пропорционална је индуктивности завојнице и брзини промене струје кроз њу.

На пример, израчунајмо индуктивни отпор завојнице са индуктивношћу од 1 Х, која је укључена у коло са фреквенцијом струје од 50 Хз:

Ако је фреквенција куглице била 5000 Хз, онда би отпор истог намотаја био приближно 31 400 ома. Подсетимо се да је омски отпор жице завојнице обично неколико ома.

Из наведених формула је очигледно да се промене струје кроз калем и напона у њему јављају у различитим фазама, а фаза струје је увек мања од фазе напона на пи/2. максимална струја се јавља четвртину периода касније од почетка максималног стреса.

Код индуктивног отпора струја заостаје за напоном за 90 степени због кочионог ефекта самоиндукованог ЕМФ-а, који спречава да се струја промени (и повећање и смањење), па се максимална струја уочава у колу са калемом касније. од максималног напона.

Комбиновано деловање завојнице и кондензатора

Ако спојите калем са кондензатором у серију са колом наизменичне струје, онда ће напон завојнице унапредити напон кондензатора у времену за пола периода, односно за 180 степени у фази.

Капацитивни и индуктивни отпор се називају реактанти… Енергија се не троши у реактивном отпору као у активном отпору. Енергија ускладиштена у кондензатору се периодично враћа назад у извор када електрично поље у кондензатору нестане.

Исто је и са калемом: како магнетно поље завојнице ствара струја, енергија у њему се акумулира током једне четвртине периода, а током следеће четвртине периода враћа се извору. У овом чланку смо говорили о синусоидној наизменичној струји, за коју се ови прописи стриктно поштују.

У синусоидним колима наизменичне струје називају се индуктори са језгром гушећи сесе традиционално користе за ограничавање струје. Њихова предност у односу на реостате је у томе што се енергија не расипа у огромним количинама као топлота.