Активни отпор и индуктор у колу наизменичне струје

Узимајући у обзир АЦ коло које садржи само индуктивни отпор (погледајте чланак «Индуктор у колу наизменичне струје»), претпоставили смо да је активни отпор овог кола нула.

У ствари, и жица самог намотаја и спојне жице имају мали, али активан отпор, тако да коло неизбежно троши енергију извора струје.

Због тога је при одређивању укупног отпора спољашњег кола потребно додати његове реактивне и активне отпоре. Али немогуће је додати ова два отпора која су различита по природи.

У овом случају, импеданса кола наизменичном струјом се налази геометријским сабирањем.

Конструисан је правоугли троугао (види слику 1), чија је једна страна вредност индуктивног отпора, а друга вредност активног отпора. Жељена импеданса кола је одређена трећом страном троугла.

Слика 1. Одређивање импедансе кола које садржи индуктивни и активни отпор

Импеданса кола је означена латиничним словом З и мери се у омима. Из конструкције се види да је укупни отпор увек већи од индуктивног и активног отпора одвојено.

Алгебарски израз за укупан отпор кола је:

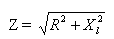
где је З - укупни отпор, Р - активни отпор, КСЛ - индуктивни отпор кола.

Дакле, укупан отпор кола наизменичном струјом, који се састоји од активног и индуктивног отпора, једнак је квадратном корену збира квадрата активног и индуктивног отпора овог кола.

Охмов закон пошто се такво коло изражава формулом И = У / З, где је З укупан отпор кола.

Хајде сада да анализирамо колики ће бити напон ако коло, поред и и фазног померања између струје и индуктивности, има и релативно велики активни отпор. У пракси, такво коло може бити, на пример, коло које садржи индуктор са гвозденим језгром намотан танком жицом (високофреквентна пригушница).

У овом случају, фазни помак између струје и напона више неће бити четвртина периода (као што је то било у колу са само индуктивним отпором), већ много мање; а што је већи отпор, то ће резултирати мањим помаком фазе.

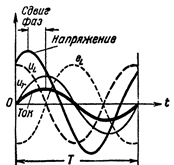
Слика 2. Струја и напон у колу које садржи Р и Л.

Сада она сама ЕМФ самоиндукције није у антифази са напоном извора струје, јер је померен у односу на напон не за пола периода, већ за мање.Поред тога, напон који ствара струјни извор на прикључцима завојнице није једнак емф самоиндукције, већ је већи од њега за количину пада напона у активном отпору жице завојнице. Другим речима, напон у завојници се ионако састоји од две компоненте:

• тиЛ- реактивна компонента напона, која балансира ефекат ЕМФ од самоиндукције,

• тиР- активна компонента напона која ће савладати активни отпор кола.

Ако велики активни отпор повежемо серијски са калемом, фазни помак ће се толико смањити да ће тренутни синусни талас скоро сустићи синусни талас напона и разлика у фазама између њих ће бити једва приметна.У овом случају, амплитуда члана и биће већа од амплитуде појма.

Слично томе, можете смањити фазни помак, па чак и потпуно га смањити на нулу ако на неки начин смањите фреквенцију генератора. Смањење фреквенције ће резултирати смањењем ЕМФ самоиндукције, а самим тим и смањењем фазног помака између струје и напона у колу изазваног тиме.

Снага АЦ кола које садржи индуктор

Коло наизменичне струје које садржи калем не троши енергију извора струје и да у колу долази до процеса размене енергије између генератора и кола.

Хајде да сада анализирамо како ће ствари бити са снагом коју троши таква шема.

Снага која се троши у колу наизменичне струје једнака је производу струје и напона, али пошто су струја и напон променљиве величине, тада ће и снага бити променљива.У овом случају можемо одредити вредност снаге за сваки тренутак у времену ако помножимо тренутну вредност са вредношћу напона која одговара датом тренутку у времену.

Да бисмо добили график снаге, потребно је да помножимо вредности праволинијских сегмената који дефинишу струју и напон у различито време. Таква конструкција је приказана на сл. 3, а. Испрекидани таласни облик п нам показује како се мења снага у колу наизменичне струје које садржи само индуктивни отпор.

За конструисање ове криве коришћено је следеће алгебарско правило множења: Када се позитивна вредност помножи са негативном вредношћу, добија се негативна вредност, а када се помноже две негативне или две позитивне вредности, добија се позитивна вредност.

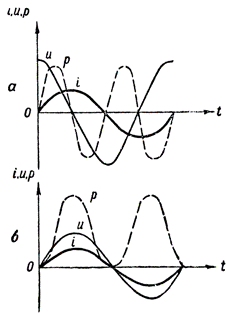
Слика 3. Графикони снаге: а — у колу које садржи индуктивни отпор, б — такође, активни отпор

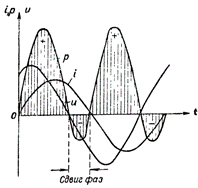
Слика 4. Графикон снаге за коло које садржи Р и Л.

Крива снаге у овом случају лежи изнад временске осе. То значи да нема размене енергије између генератора и кола и стога струју коју генератор доводи у коло потпуно троши коло.

На сл. 4 приказује дијаграм снаге за коло које садржи и индуктивни и активни отпор. У овом случају долази и до обрнутог преноса енергије из кола у извор струје, али у много мањој мери него у колу са једним индуктивним отпором.

Након прегледа горњих графикона снаге, закључујемо да само фазни помак између струје и напона у колу ствара "негативну" снагу.У овом случају, што је већи помак фазе између струје и напона у колу, то ће коло трошити мање енергије, и обрнуто, што је мањи помак фазе, то је већа снага коју коло троши.

Прочитајте такође: Шта је напонска резонанца